.
.
Structure in Nature
The discovery and understanding of first-principles is the subject of Pearce’s first book, Structure in Nature is a Strategy for Design, The MIT Press, 1978, 1990.
The book examines how such principles inform the structure and form of possible design systems. This work comprises the theoretical basis of Pearce’s work in the design and engineering of state-of-the-art architectural projects. These principles apply to all of Pearce’s work including building applications and high-performance ergonomic seating.
The following images of natural structure include both macro and micro-photographs. These patterns can be easily discerned and represent manifestations of least effort structures. Recurring geometries are revealed that are common in nature regardless of scale. Such patterns of form and structure occur at the macroscopic, microscopic, and sub-microscopic levels. The material presented here is fully developed in Pearce’s book.
Soap Bubbles
Soap bubble arrays form polyhedral packings in which shared faces (cell partitions) meet in sets of three at 120 degrees, and edges meet tetrahedrally in sets of four at 109 degrees 28 minutes. In such schemes surface to volume is minimized. The forces of surface tension govern cellular form, and the conditions of minimal potential energy are satisfied. The topology of the soap bubble array thus becomes the quintessential prototype for all macro and microcellular morphology in nature, both organic and inorganic.


Cracked Mud
Cracked mud is characteristic of planar or quasi-planar cellular aggregates in nature. Typically partition edges meet in sets of three, approximating the 120-degree angle of the tiling of regular hexagons. Indeed, the average number of sides of the cells is six. That is the cell shape on average is hexagonal.

Philodendron Leaf Surface
The topology of the veins of a leaf surface typically follows the same minimum energy patterns of the hexagonal network, not unlike the pattern exhibited by the cracked mud example.

Honey Comb
The honeybee constructs a remarkably uniform structure to store his product. The iconic hexagonal honeycomb minimizes surface to volume, saving material and energy in the process. In essence, it stores the greatest amount of honey with the least amount of bee wax. This two-sided structure is optimized design at its most elegant.


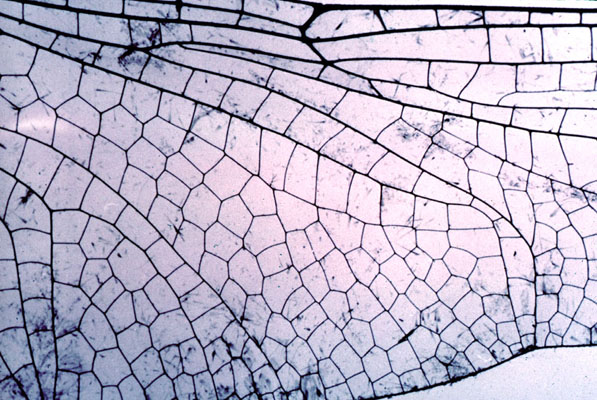
Dragonfly Wing
Like the leaf structure and the pattern of cracked mud, the dragonfly wing exhibits the same hexagonal partitioning tendencies as it manifests an arrangement of least effort. The geometry of biological patterns such as this is more complex because of the hierarchical growth stages that determine their form. The form is truly a diagram of forces.
Snow Crystals
There are an infinite number of planar snow crystal configurations, all of which are found to have the symmetry of a regular hexagon. The molecular structure of the snow crystal governs these geometric options as the environmental forces are diagramed to produce infinite diversity of form. This is an archetypal example of a minimum inventory/maximum diversity system.

Molecular Structure of Platinum
This field ion microscope photograph of platinum (600,000x) reveals a dense packing of atoms. This close-packed geometry, which is typical of metal structures, contributes to the characteristic strength of metal materials. Once again, forces of least energy govern such morphology.

Closest Packing and Triangulation
Equal circles or regular hexagons can be closest packed in a plane. When centers of close-packed circles or hexagons are joined to nearest neighbors a grid of equilateral triangles is formed. The hexagonal array diagrams the geometry of the honeycomb, with its low surface to volume (and in three dimensions the soap bubble array), and the closest packed array of circles corresponds to the dense packing of atoms in metal structures. As a physical system triangulated frameworks manifest the only inherently stable geometry. This property of inherent stability is correlated to the attributes of these natural structures and accounts for the high strength to weight of three-dimensional truss systems. It is a pattern of least energy.

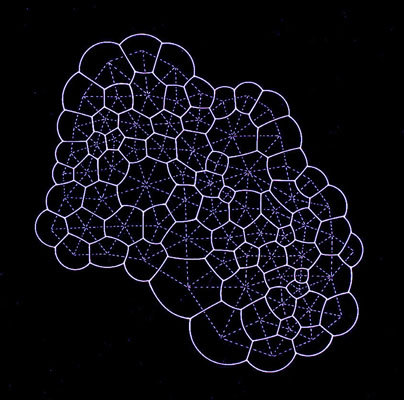
Cellular Froth
Seemingly random arrays of cells such as bubbles or the cells in plants or animals, are actually arrangements of least energy and manifest the most stable possible morphology. Joining the centers of such arrays give rise to a triangulated network, just as in the case of the tiling of regular hexagons. Inherent stability is achieved while surface to volume is minimized. This rigorous structure appears random because of the differential volume of the cells. Although, because of this differential volume, cells have different numbers of sides in this planar example, the average cell shape will have six sides. This again corresponds to the number of sides of a regular hexagon. Furthermore, angles measured as tangents at the points of intersection will be shown to be 120 degrees, the face angle of the regular hexagon. Randomness is not an appropriate characterization of this morphology.
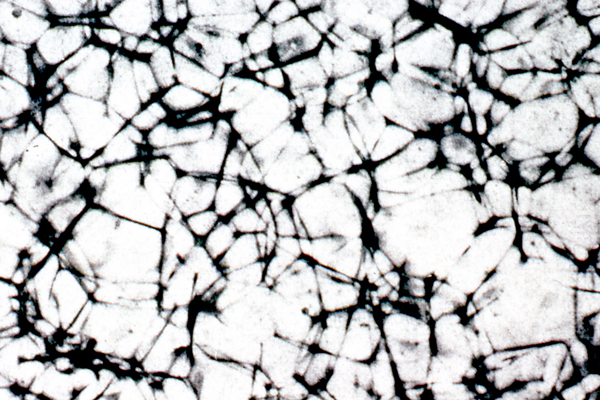
Aluminum –tin Alloy. X-ray microradiograph
A dark polyhedral network is formed by the tin surrounding the light-shaded cells (crystals) of aluminum. This micro-photograph is virtually indistinguishable from a soap bubble froth as seen with the unaided eye. This is true to the extent that the vertices are typically surrounded by four edges (four cells) meeting at approximately 109.5 degrees as they do in soap froth.
Basalt Columns
These hexagonal columns of basalt are formed by the cooling of volcanic rock. Somewhat like cracked mud, they form patterns of 3-rayed hexagonal intersections, although typically more uniform than cracked mud. In both cases, nature’s pattern of least energy is the driving force.


River Meanders
The meandering of rivers is caused as the flowing water seeks a trajectory of least resistance – of least energy. Bertrand Russell called this the law of cosmic laziness.


Watermelon
In this detail of the watermelon is exhibited a pattern of two vertices with edges (lines) meeting at approximately 120 degrees. Of course, this is the typical angle of the bee’s honeycomb and is a common angle throughout the natural structure. Once again the tendency to seek patterns of least energy appears, in this case, to the naked eye as the cells of the watermelon organize themselves in a familiar pattern.







