.

.

Morphology – The Shape of Things

A major component in the understanding of first principles is the study of three-dimensional form and the factors that govern the shape of things. This study of shape, or morphology, involves the fundamental principles of spatial geometry that govern optimum form and structure.

The fundamentals of spatial geometry account for possible arrangements of elements or components in three-dimensional space. The natural structure is constrained by such principles at the macro and micro levels. Spatial geometry is scale-independent. A triangle is a triangle regardless of how large or small it may be. Knowledge of such principles has direct applicability to the design of architectural structures, particularly from a systems building perspective.

Over 80 optimized space truss structures designed and built by Pearce have benefitted directly from these morphological investigations. The pinnacle of this work, and the most recent of Pearce’s building design efforts, is the Hólos House (aka Pearce Ecohouse). Indeed, the study of natural structure in general, with an emphasis on morphology, comprises the theoretical underpinnings of this work in advanced structural and architectural design.

Examples of fundamental spatial geometries:

Platonic Polyhedra

There are five possible polyhedra bounded by regular polygons. These are known as the regular polyhedra. Since they were part of Plato’s cosmology, they have been known for at least 2500 years. It is likely that knowledge of this geometry goes back in history for many thousands of years. This is a phenomenal observation. If regular polygons (equal angle and edge length) of a single type are used to assemble closed volumes there are only these five configurations – certainly the first principle. Although this can be proven mathematically, this truth is empirically obvious.

Archimedean Polyhedra

These configurations are similar to the regular polyhedra, with the proviso that more than one type of regular polygon may be used to assemble a volume. These polyhedra were studied by Archimedes, and are commonly known as the semi-regular polyhedra. Like regular polyhedra, they have been known for thousands of years. There are only 13 possible semi-regular polyhedra, and like the regular polyhedra, this truth is empirically obvious. Shown here are only six of the thirteen semi-regular, along with three of the regular polyhedra. Combinations of these can fit together in various combinations without gaps to form space-filling aggregates. Of the regular polyhedra, only the cube can fill space by itself, and of the semi-regular polyhedra, only the truncated octahedron can fill space by itself.

These systems of spatial subdivision occur throughout nature at the molecular level as they govern the geometry of atomic arrangements. The regular and semi-regular polyhedra are important for design as they define systematic spatial options beyond the orthogonal bias that dominates most buildings.

Spatial Networks

The Truncated Octahedron

Orderly spatial subdivisions can be visualized as points in space, as volumes packed, or as networks of linear members. All three of these morphologies can define the exact same geometry. In this case, a space-filling of truncated octahedral creates a uniform spatial network. The nodes that hold the network together are explained in Pearce’s book, Structure in Nature is a Strategy for Design. Of all the regular and semi-regular polyhedra that fill space, the truncated octahedron does so with the least surface area per unit of volume. Because of this, it is the archetype for least energy cellular aggregates.

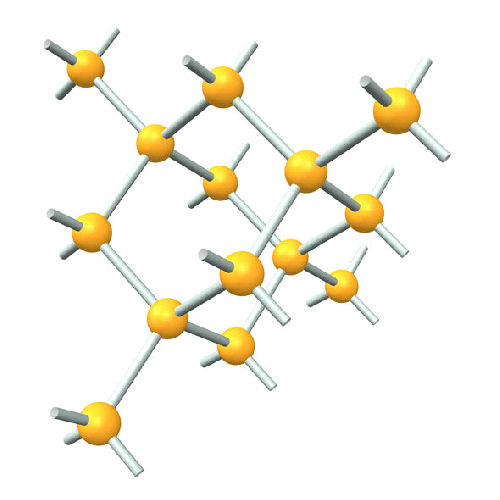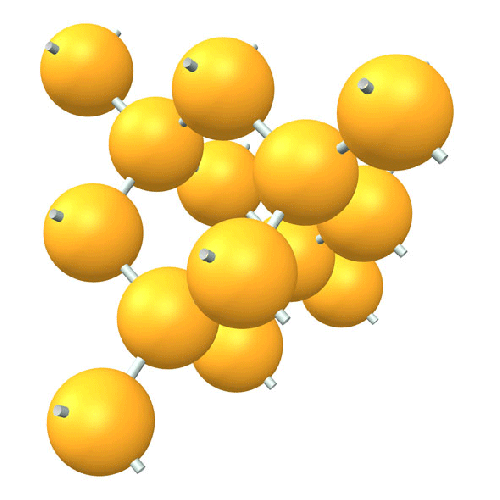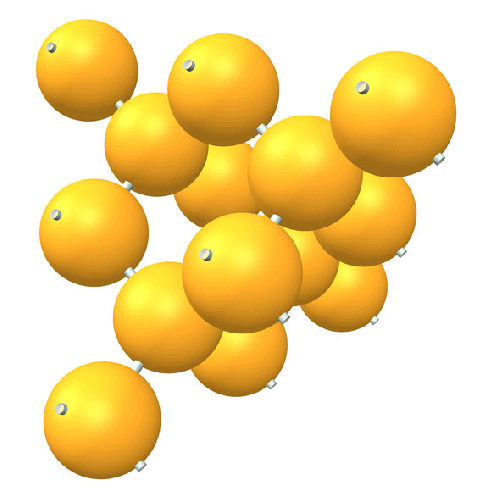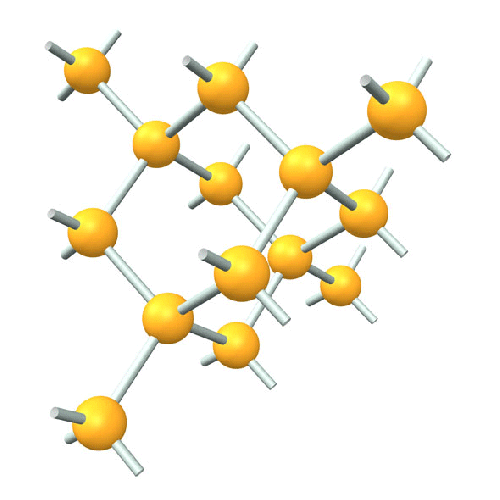
Diamond Network 

The diamond crystal is composed of a uniform spatial assembly of carbon atoms. The bond angles are everywhere 109° 28’. This geometry can be clearly represented as a network in which network members meet uniformly around vertices (nodes) at 109° 28’. The centers of carbon atoms of the diamond crystal are positioned at these nodes of this network.

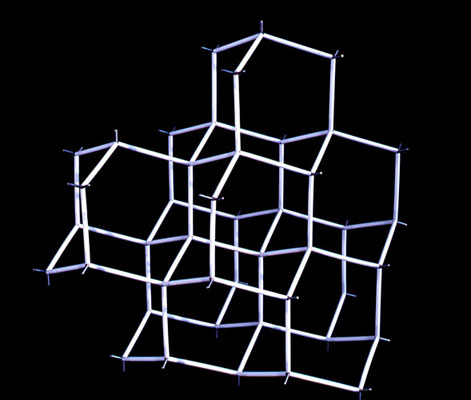
Uniform Networks

There are an infinite variety of possible ordered spatial networks. Some are more ordered than others, and some may be highly uniform but from certain angles of view can appear completely random. The most uniform networks will have all their nodal geometries identical. Two examples are shown here in which three branches meet in a plane at 120° at every node in the network. Such networks can be repeated to infinity with the same recurring geometry. The previously shown diamond network is also a uniform infinite network.

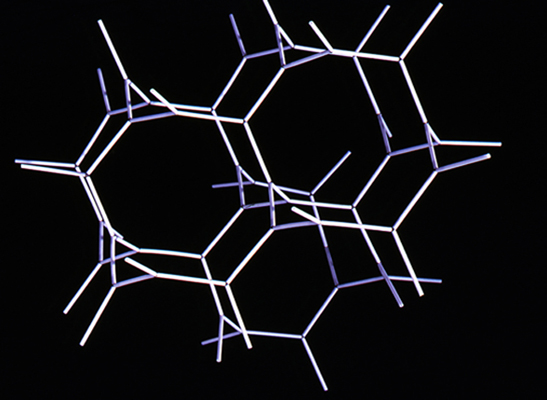
Networks of Cells

Polyhedral cellular structures are found throughout nature. This includes animated and inanimate substances. This can range from the shapes of cells in plants, animals, metals, minerals, and even soap bubbles. The volumes of such aggregated cell shapes tend to be bounded by pentagons and hexagons, although they are not regular polygons. Perhaps more important to the underlying structure of these cellular aggregates is that the edges shared between them meet at vertices (nodes) everywhere in sets of four at approximately 109 degrees 28 minutes. This is a manifestation of patterns of least energy in which the ratio of surface to volume is always minimized (see Structure in Nature).

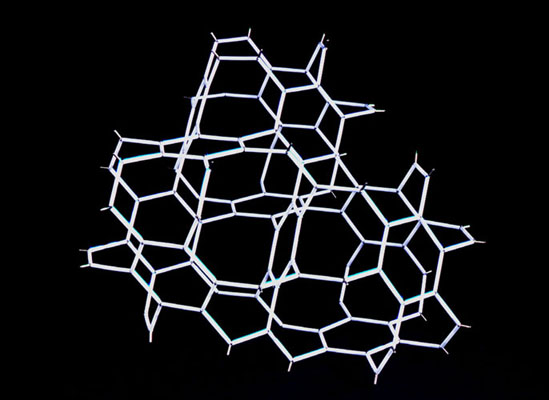
Complex Networks

A network morphology is created in which all possible spatial networks coexist within a particular infinite class of possibilities. Each distinct infinite network can be considered a sub-set of this universal network. This universal network repeats to infinity with two types of nodal geometry. There are six nodes with 6 branches meeting for every single node with 26 branches meeting in an infinite array. The images show an arbitrary segment of the infinite array.

Triangulated Networks

Triangulated geometries are the only ones that form inherently stable structures. Because of this, it is important to consider repeating triangulated networks. The study of three-dimensional triangulated networks has led Pearce to a deep understanding of intrinsically stable high-strength to material weight structurally autonomous structures. Such structures offer material efficiencies while at the same time providing structural redundancies. The combination of the intrinsic stability and structural redundancy of these triangulated structures offers important advantages for the design of buildings. With this approach, catastrophic failure due to any sort of locally concentrated internal or external exacerbations can be mitigated. This results in safer and more resilient buildings.

The images show triangulated geometries that can be infinitely repeated. Such networks can be derived from uniform networks, space-filling of polyhedra, open packings of polyhedra, and periodic minimal surfaces.

Saddle Polyhedra

A polyhedron is defined as a volume bounded or enclosed by flat polygonal faces. There is another class of polyhedra discovered and named by Pearce, which he calls saddle polyhedra. These are bounded by non-planar (curved) surfaces derived from skew polygons. As the name suggests the skew polygon is not flat as are typical polygonal geometries. The surface defined by the skew polygon is considered a minimal surface and is generally saddle-shaped. Although there can be an infinite number of skew polygons only certain ones can fit together to enclose a volume.

The most important saddle polyhedra are those that are derived from repeating uniform networks. When this is done the derived saddle polyhedra create space-filling geometries. For example, figure FP-25 is based on the three connected uniform networks of figure FP-15. A space-filling saddle polyhedron with three curved faces is bounded by a skew polygon of 10 edges (decagon). This can be called a trihedron (three faces). There can be saddle polyhedra with more than one type of face and even some that combine saddle faces with flat polygonal faces.

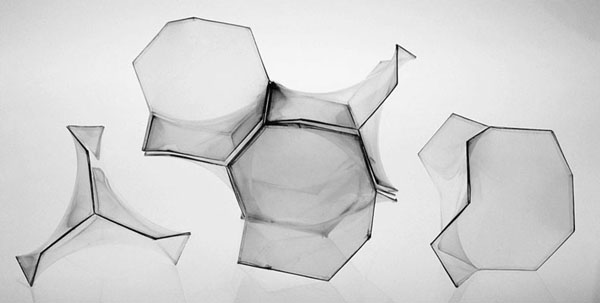
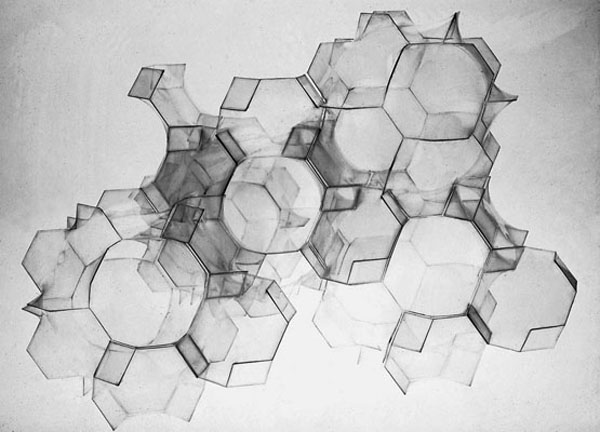
Minimal Surfaces

Saddle polygons defined by skew polygons occur in another important infinitely repeating geometric system. These are known as infinite periodic minimal surfaces. They can be derived by systematically repeating certain saddle polygons to create smooth continuous surfaces that can theoretically repeat to infinity. These continuous surfaces create three-dimensional labyrinths that map the molecular geometry of certain substances such as the diamond crystal. Such structures can also be derived directly from certain saddle polyhedral space-filling systems.

.

.
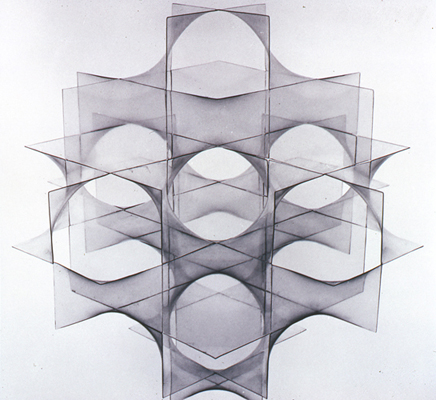